Um (Netz)Wechselspannungen
umzuwandeln sind 50-Hz-Transformatoren immer noch die einfachsten und
meistens auch billigsten Spannungswandler. Auch im Zeitalter von
Schaltnetzteilen und schnellen Leistungshalbleitern sind die
50-Hz-Transformatoren nicht aus der Elektronik wegzudenken.
Schließlich handelt man sich mit diesen Bauteilen keinerlei
Probleme mit Oberwelleneinstreuung in das 230-Volt-Netz oder mit
hochfrequenten Abstrahlungen ein. In puncto Zuverlässigkeit und
Unempfindlichkeit gegen Überspannungsspitzen dürften solche
Trafos noch unübertroffen sein.
Die Funktionsweise eines
Trafos steht zwar in fast jedem Buch, ich möchte sie aber
trotzdem noch einmal zusammenfassen: Die Primärspule wird an
eine Wechselspannung, z.B. 230 Volt Netzspannung, gelegt. Der
Spulenstrom erzeugt ein Magnetfeld, das in der Primärspule
wiederum eine Spannung induziert. Damit der Spulenstrom nicht ins
Unermessliche steigt, muss die in der Primärspule
induzierte Spannung etwa genauso groß sein wie die angelegte
(Netz)Spannung. Die angelegte Spannung erzwingt also das sie
induzierende Magnetfeld. Gelingt es, eine zweite Spule, die
Sekundärspule, so anzubringen, dass sie vom gleichen
magnetischem Fluss durchflossen wird, wird auch in ihr die
gleiche Spannung pro Windung induziert wie in der Primärspule.
Wird die Sekundärspule belastet, erzeugt sie ein magnetisches
Gegenfeld, das das primäre Magnetfeld abschwächt. Da das
primäre Magnetfeld in seiner Stärke aber durch die
angelegte Primärspannung erzwungen wird, kann es nur durch einen
der sekundären Belastung entsprechenden zusätzlichen
Primärstrom aufrecht erhalten werden. So lässt sich
dann Leistung von der Primär- auf die Sekundärspule
übertragen. Beim Bau eines Trafos gibt es aber noch praktische
Probleme: Zum einen sind bei 50 Hz recht hohe Magnetfeldamplituden
erforderlich, um eine nennenswerte Spannung in der Spule zu
induzieren und zum anderen ist es sehr schwierig, dafür zu
sorgen, dass durch beide Spulen der gleiche magnetische Fluss
fließt. Beide Probleme lassen sich durch Verwendung eines
geschlossenen Kernes aus Weicheisen weitgehend lösen. Durch die
hohe Pemeabilität des Eisens (Durchlässigkeit bzw.
Leitfähigkeit für magnetische Felder) ist zum Aufbau eines
magnetischen Flusses bestimmter Stärke nur etwa ein
zehntausenstel des Stromes erforderlich, der bei einer Luftspule
nötig wäre. Dadurch ist der Bau von 50-Hz-Transformatoren
überhaupt erst möglich. Die hohe Durchlässigkeit des
Weicheisens für magnetische Felder sorgt außerdem auch
dafür, dass kaum eine Feldlinie die Abkürzung durch
die Luft nimmt und so praktisch der gesamte magnetische Fluss
durch den Eisenkern laufen muss. Damit werden automatisch alle
auf dem Kern befindliche Spulen vom gleichen Fluss durchflossen.
Die Verhältnisse sind leider nicht mehr so ideal, wenn die
Sekundärspule des Transformators mit einem Strom belastet wird.
Das von der Sekundärspule erzeugte Gegenmagnetfeld reduziert die
effektive magnetische Leitfähigkeit des Eisens und veranlasst
die eine oder andere Feldlinie dazu, doch eine Abkürzung durch
die Luft und an der Sekundärspule vorbei zu nehmen. Dieser
unerwünschte, als Streuung bezeichnete Effekt ist umso stärker,
je weiter die Spulen räumlich voneinander entfernt sind. Die
praktische Auswirkung der Streuung besteht darin, dass sich zu
dem ohnehin vorhandenen ohmschen Widerstand der Kupferdrähte
noch ein induktiver Anteil, die sogenannte Streuinduktivität,
hinzuaddiert. Die Streuung erhöht also den Innenwiderstand der
Sekundärspannung und damit auch ihre Lastabhängigkeit.
Ein weiteres Problem sind die im Eisenkern induzierten Spannungen und die dadurch fließenden Wirbelströme. Würde man einen massiven Eisenkern aus gewöhnlichem Weicheisen verwenden, würde sich der Wirkungsgrad des Transformators nicht nur wesentlich verschlechtern, sondern der Eisenkern würde sich stark erwärmen und erhebliche Kühlungsprobleme verursachen. Da die Induktionsspannungen im Kern unvermeidlich sind, lassen sich die Wirbelströme nur durch eine Reduktion der elektrischen Leitfähigkeit des Eisens veringern. Die wirkungsvollste Reduktion der Leitfähigkeit erreicht man durch die Aufteilung des Kernes in möglichst viele Einzelbleche. Die Bleche liegen in Richtung der magnetischen Feldlinien, sodass die Leitfähigkeit des Kernes für das magnetische Feld nicht beeinträchtigt wird. Die Wirbelströme jedoch, die senkrecht zu den magnetischen Feldlinien fließen, können die Grenzen zwischen den Blechen, die gegeneinander isoliert sind, nicht überwinden. Es können dann nur noch die wesentlich kleineren Wirbelströme innerhalb der einzelnen Bleche fließen. Diese restlichen Wirbelströme lassen sich nochmals reduzieren, indem die elektrische Leitfähigkeit des Eisens durch Zugabe von einigen Prozent Silizium deutlich herabgesetzt wird.
1.1 Die gebräuchlichen
Kernbauformen
Die Kernbauformen sind
weitgehend standardisiert und werden nach Blechform und Größe
bezeichnet. Folgende Bauformen sind dabei gebräuchlich:
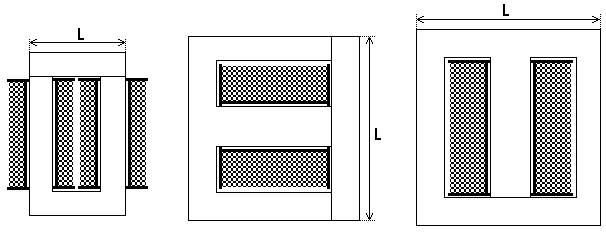
Bild 1.1 A UI-Kern Bild 1.1 B EI-Kern Bild 1.1 C M-Kern
Bild 1.1 A zeigt den einfachen UI-Kern, der, wie der Name schon sagt, aus einzelnen Blechen in U- und I-Form besteht. Bei dem UI-Kern können beide Schenkel mit einem Spulenkörper versehen werden. Am einfachsten wäre es, auf dem einen Spulenkörper die Primär und auf dem anderen die Sekundärspule unterzubringen. Leider erkauft man sich mit dieser Vereinfachung eine erhebliche Zunahme der Streuung, was den Innenwiderstand der Ausgangsspannung entsprechend erhöht. UI-Kern-Transformatoren werden daher fast immer symmetrisch gebaut, sodass sich Primär- und Sekundärspule je zur Hälfte auf dem einen und dem anderen Spulenkörper befinden. Diese Aufsplittung erhöht natürlich die Herstellungskosten. Der Vorteil ist die flache Bauweise (Einsatz für Flachtransformatoren) und die gute Ausnutzung des Eisenkernes, der fast vollständig umwickelt ist. Die aus einem U-und I-förmigen Blech bestehenden Schichten werden üblicherweise abwechselnd gegensinnig in die Spulenkörper geschoben. Das erhöht die Stabilität des Blechpaketes und verringert vor allem den effektiven Luftspalt des Kernes. In Bild 1.1 B ist der bei Kleintransformatoren gebräuchlichste EI-Kern dargestellt. Wie beim UI-Kern sind auch beim EI-Kern die Einzelbleche gegensinnig angeordnet. Der Vorteil des EI-Kernes besteht darin, dass alle Wicklungen preiswert auf einen Spulenkörper gewickelt werden können. Je nach Anforderung werden die Wicklungen übereinander (geringe Streuung, niedriger Innenwiderstand) oder in zwei getrennten Kammern nebeneinander (gute Schutztrennung) angeordnet. Zur Vereinfachung der Herstellung wird auch oft das E- und das I-Paket auf den Spulenkörper zusammengedrückt und an den Außenkanten verschweißt. Da die Schweißnaht nur entlang der Außenkante verläuft und so keinen geschlossenen Ring um den Kern herum bildet, können dort auch keine nennenswerten Wirbelströme fließen. EI-Kern-Transformatoren haben mit den marktüblichen Blechabmessungen, im Gegensatz zu den relativ flachen UI-Kern-Transformatoren, eher eine kubische Bauform.
Eine Verbesserung des EI-Kernes, der M-Kern, ist in Bild 1.1 C zu sehen. Die Bleche einer Schicht bestehen jetzt nur noch aus einem Stück. Der magnetische Fluss muss hier nur noch den einen Luftspalt im Mittelschenkel überwinden. Dieser ist dazu noch minimal, weil die Außenschenkel kein Auseinanderziehen des Bleches erlauben. Die Montage der Bleche ist dafür etwas schwieriger; vieleicht eine Ursache dafür, dass die M-Kerne etwas aus der Mode gekommen sind. Anstatt den Kern aus einzelnen Blechen zusammenzuzetzen, kann man ihn auch aus einem langen Band wickeln. Dies vereinfacht nicht nur die Herstellung des Kernes, sondern veringert, wegen der Ähnlichkeit von Feldlinien- und Blechverlauf, auch dessen Streufelder. In Bild 1.1 D ist ein sogenannter Schnittbandkern zu sehen. Um das Blechpaket in einen Spulenkörper schieben zu können, muss es zunächst aufgeschnitten werden (daher der Name). Damit sich beim Zusammenbau kein wesentlicher Luftspalt bildet, werden die Schnittflächen der Kernstücke plangeschliffen und mit Hilfe eines Stahlspannbandes um den Kern herum dauerhaft zusammengepresst. Übliche Bauformen sind sowohl die in Bild 1.1 D gezeigte, aus vier Kernstücken bestehende Version mit doppeltem Außenschenkel, die dem EI- oder M-Kern entspicht als auch die dem UI-Kern entsprechende einfache Version mit zwei Spulenkörpern und nur zwei Kernstücken. Schnittbandkerne findet man nur noch selten, da sie von den kostengünstigen und besseren Ringkernen weitgehend verdrängt wurden.
Bild 1.1 D Schnittbandkern Bild 1.1 E Ringbandkern
1. Der in Bild 1.1 E gezeigte Ringkern ist eigentlich der ideale Kern. Im Gegensatz zum Schnittbandkern wird das Eisenband im Ringkern kreisrund gewickelt und nicht durchgeschnitten. Da die magnetischen Feldlinien einer Ringluftspule (Toroid) sowieso dort verlaufen würden, wo sich der Eisenkern befindet, können sie auch keine Abkürzungen außerhalb der Spule nehmen. Der Ringkerntransformator ist daher bei gleichmäßiger Bewicklung nahezu streufeldfrei. Dies bedeutet jedoch nicht, dass der Ringkerntransformator keine Streuinduktivität besitzt. Die doppelte Bedeutung des Begriffes Streufeld tritt hier besonders deutlich zu Tage. Während sich die meisten Anwender nur für das nach außen dringende Störstreufeld interessieren, das vor allem in Audiogeräten unangenehme Brummspannungen induziert, ist das nicht nach außen dringende, ebenfalls ringförmige Streufeld in und zwischen den Primär- und der Sekundärwicklungen für die Streuinduktivität verantwortlich. Wegen der dichten Anordnung von Primär- und Sekundärspule ist die Streuinduktivität allerdings niedriger als bei allen anderen Kernformen. Dafür ist auch die Isolation großflächiger und etwas problematischer, vor allem bei hohen Spannungen. Ringkerntransformatoren werden deshalb vorwiegend für Anwendungen bis 230 Volt Netzspannung eingesetzt. Für höhere Spannungen verwendet man hauptsächlich EI- oder UI-Kerne. Für die Bewicklung von Ringkernen sind spezielle Wickelmaschinen erforderlich. Erst solche Maschinen erlauben eine wirtschaftliche Herstellung dieser Transformatoren.
1.2 Die Dimensionierung
von 50-Hz-Transformatoren
Ein Transformator ist dann
optimal ausgenutzt, wenn das Eisen im Kern gerade noch nicht in
die Sättigung gerät. In diesem Fall wird der maximal
mögliche magnetische Fluss und somit auch die maximal
mögliche Induktionsspannung erreicht. Die für eine
bestimmte Spannung erforderliche Windungszahl ist dann minimal und
der bei vorgegebenenm Wicklungsquerschnitt mögliche
Drahtdurchmesser maximal. Mit einer niedrigeren Windungszahl würde man
den Kern unweigerlich in die Sättigung fahren; die stark
reduzierte Induktivität der Primärspule während der
Sättigung führt zu einem schnell ansteigenden Strom, der,
zusammen mit den Sättigungsverlusten im Eisenkern, zur
Überlastung des Transformators führt. Erhöht man die
Windungszahl, wird der Draht von Primär- und Sekundärspule
länger und auch dünner (er muss dünner werden,
damit er auf den begrenzten Wicklungsquerschnitt passt). Dadurch
erhöht sich nicht nur die Streuinduktivität, der
zusätzliche Drahtwiderstand führt auch zu einer geringeren
Belastbarkeit des Transformators.
1.2.1 Die
erforderliche Kerngröße eines Transformators
Die Größe des
Trafos für eine geforderte Leistung ist ein Erfahrungswert. Für
die standardisierten Kernformen sind diese Werte bei den
Trafoherstellern aber in etwa bekannt. Im Zweifelsfall nimmt man dann
den nächstgrößeren Kern. Wer nicht im Besitz dieser
Erfahrungswerte ist, kann sich auch mit den Ähnlichkeitsgesetzen
weiterhelfen. Dazu sucht man sich einen bekannten Standardkern mit
bekannter Leistung im mittleren Bereich aus, z.B. EI60/21 mit ca. 20
VA. Wegen des induktiv bedingten Blindleistungsanteiles der vom Trafo
aufgenommenen Gesamtleistung wird die Leistung üblicherweise als
Scheinleistung mit der Abkürzung VA angegeben. Eine nennenswerte
Abweichung der Scheinleistung von der tatsächlich erzielbaren
Ausgangswirkleistung findet man vor allem bei Trafos mit sehr kleiner
Leistung und/oder großer Streuinduktivität (Streutransformatoren). Im
Normalfall kann das VA direkt durch Watt
ersetzt werden. Die Kernaussage der Ähnlichkeitsgesetze besteht
darin, dass bei einer maßstabgetreuen Vergrößerung
bzw. Verkleinerung eines Originals um den Faktor k sich alle Strecken
um das k-fache vergrößern bzw. verkleinern. Dies ist
eigentlich selbstverständlich und leicht einzusehen, hat aber
manchmal erstaunliche Konsequenzen. Als unmittelbare Folgerung aus
dieser Tatsache ergibt sich, dass sich alle Flächen um das
k2-fache, alle
Volumina und Massen um das k3 -fache vergrößern
bzw. verkleinern. Will man einen Trafo
um das k-fache vergrößern, vergrößert sich die
Querschnittsfläche des Eisenkerns, also auch der maximale
magnetische Fluss um das k2 -fache. Die nötigen
Windungszahlen reduzieren sich dann um das
k2-fache, der
Windungsumfang erhöht auf das k-fache, die Drahtlänge der
Wicklungen reduziert sich daher um das k-fache. Gleichzeitig steht
jetzt, bei einer um k2-fach
reduzierten Windungszahl, der k2-fache
Wicklungsquerschnitt zur Verfügung. Der Drahtquerschnitt kann
somit um das k4-fache erhöht werden. Wegen der
Verlängerung des
Windungsumfanges
bei gleichzeitiger Reduktion der Windungszahl um das k2
-fache reduziert sich der Drahtwiderstand schließlich um das
k5-fache. Die
zulässige Verlustleistung ist in etwa proportional zur
Oberfläche, erhöht sich also um das k2-fache.
Da die Verlustleistung mit dem Quadrat des Laststromes, also auch mit
dem Quadrat der Übertragungsleistung wächst, erlaubt die
Reduktion des Drahtwiderstandes um das k5-fache
eine Erhöhung der Übertragungsleistung um das k2,5-fache.
Die Zunahme der Oberfläche und zulässigen Verlustleistung
um k2 erlaubt
eine weitere Erhöhung der Übertragungsleistung um das
k-fache. Daraus ergibt sich folgende allgemeine Umrechnungsregel:
Werden die Abmessungen
eines Transformators bei konstanter Frequenz und Bauform mit dem
Maßstab k multipliziert, multipliziert sich die erzielbare
Übertragungsleistung mit dem Faktor k3,5.
Erstaunlich an diesem Ergebnis ist, dass bei Vergrößerung eines Trafos die Leistung stärker steigt als Volumen und Masse. Die Eisenverluste sind allerdings volumenproportional. Da bei Vergrößerung des Trafos das Volumen schneller steigt als die der Kühlung dienende Oberfläche, fallen diese Verluste mit zunehmender Trafogröße mehr ins Gewicht. Eventuell muss die Blechdicke reduziert oder der Kern zusätzlich gekühlt werden. Aus dieser Berechnung ergeben sich noch zwei weitere Vorteile großer Trafos: Während die Übertragungsleistung mit dem Faktor k3,5 steigt, erhöht sich die Verlustleistung, entsprechend der kühlenden Oberfläche, nur um k2, was eine beträchtliche Erhöhung des Wirkungsgrades großer Trafos bedeutet. Der hohe Wirkungsgrad großer Trafos geht bei kleiner Streuinduktivität aber auch mit einen niedrigen Innen- bzw. Kupferwiderstand einher. Dementsprechend ist die Ausgangsspannung kleiner Trafos lastabhängiger als die der Großen. Kleine Trafos sind aus diesen Gründen auch unempfinlicher gegen Überlastung. Sehr kleine Trafos bis etwa EI 30 sind i.d.R. sogar dauerkurzschlussfest. Die Leerlaufspannung kleiner Trafos (z.B. EI30) muss aus den gleichen Gründen mit etwa dem 1,5-fachen der Normallastspannung angesetzt werden. Der Wirkungsgrad liegt dann bei Normallast unter 70%. Fazit: große Netztrafos arbeiten also effektiver als kleine.
Ein Problem bei der Umrechnung der Leistungsklassen besteht darin, dass die Standardkerne nicht immer formgleich (ähnlich) sind. Oft wird zur Leistungsvergrößerung nur die Dicke des Blechpaketes erhöht. Im Idealfall sollte der Eisenkern im Spulenkörper aber einen quadratischen Querschnitt haben (noch besser wäre kreisrund). Bei quadratischen bzw. kreisförmigen Querschnitten lässt sich bekanntlich mit minimaler Drahtlänge die maximale Querschnittsfläche umwickeln. Für eine grobe Berechnung der zu erwartenden Übertragungsleistung ist die Ähnlichkeitsbetrachtung aber eine gute Orientierung. Soll z.B. ein Trafo mit EI-Kern eine Leistung von 80 VA (Watt) übertragen, nimmt man sich zunächst den eingangs erwähnten 20-VA-Mustertrafo EI60/21. Die Leistung soll sich also vervierfachen, d.h. k3,5 = 4 also k = 41/3,5 = 1,49. Der formgleiche Kern müsste dann eine Kantenlänge von ca. 89 mm haben. Der nächstliegende Standardkern wäre der EI88-Kern.
1.2.2 Die Berechnung
der Windungszahlen
Hat man sich erst einmal
für einen Kern entschieden, lässt sich die
erforderliche Windungszahl ganz gut berechnen. Geht man davon aus,
dass Weicheisenkerne bis zu einer magnetischen Feldstärke
von etwa 1,5 Tesla magnetisiert werden können, lässt
sich die bei 50 Hz erzielbare Umlaufspannung, das ist die
Induktionsspannung einer Windung, wie folgt berechnen: Dazu möchte
ich zunächst eine qualitative Betrachtung zum Zusammenhang
zwischen Trafospannung und Magnetfeld einfügen. Aus der
Wechselstromlehre ist bekannt, dass in einer idealen Spule die
Spannung dem Spulenstrom um 90° bzw. π/2
vorauseilt. Dies bedeutet u.a. dass der Strom im
Spannungsmaximum null und im Nulldurchgang maximal ist. Der Wert des
Stromes ist für die folgende Betrachtung und in der Praxis
belanglos. Allerdings ist er immer proportional, also auch in Phase
zum Magnetfeld. Das Magnetfeld im Eisenkern ist also im positiven
Scheitelpunkt der Wechselspannung null und baut sich bis zum
Nulldurchgang auf seinen Maximalwert auf. Bis zum negativen
Scheitelpunkt der Spannung hat es sich dann wieder bis auf null
abgebaut. Bis zum nächsten Nulldurchgang der Spannung hat es
dann den Maximalwert in umgekehrter Richtung erreicht, um sich dann
schließlich bis zum positiven Scheitelpunkt der Spannung wieder
komplett abzubauen. Der Aufbau des magnetischen Feldes einer Spule
findet also immer in einer Viertelperiode statt, beginnend im
Scheitelpunkt bis zum nächsten Nulldurchgang der Spannung. Die
Umlaufspannung einer Spule ist identisch mit der zeitlichen Änderung
des magnetischen Flusses im Eisenkern (Flussänderung pro
Sekunde). Legt man eine Spannung an die Spule an, steigt der Fluss
proportional zu Spannung und Zeit. Da sich die Spannung zeitlich
ändert, können Spannung und Zeit nicht einfach
multipliziert werden, sondern es muss ein bestimmtes Integral
ausgerechnet werden. Wer sich mit Integralrechnung nicht auskennt,
den möchte ich an dieser Stelle damit verschonen, und wer sich
damit auskennt, weis sowieso, was rauskommt. Bildlich kann man sich
jedenfalls den magnetischen Fluss als die Fläche unter der
Umlaufspannungskurve vorstellen. Eine besondere Eigenschaft der
Einheits-Sinusfunktion (Scheitelwert 1, Winkel im Bogenmaß
aufgetragen) besteht darin, dass die Fläche unter einer
Halbwelle exakt zwei ist. Die Fläche unter einer Viertelperiode
ist dementsprechend eins. Um diese noch sehr abstrakte Fläche in
die Realität zu übertragen, muss das Ganze (die Eins) noch mit dem
Scheitelwert der Umlaufspannung Û1 und der auf
das Bogenmaß 2π
bezogenen Periodendauer T der Wechselspannung multipliziert werden.
Der maximale magnetische Fluss 
im Kern errechet sich dann mit der Formel = Û1
T/2π = Û1
1/2πf.
Durch
Umstellen der Gleichung ergibt sich dann die maximale
Umlaufspannung mit Û1 = 2πf
= 2πfA
.
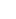Dabei
ist f die Frequenz in Hz, A die
Querschnittsfläche des Eisenkernes in Quadratmeter und 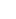die
maximale magnetische Feldstärke in Tesla (ca. 1,5 T). Setzt man
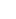die im Normalfall festen Größen f = 50 Hz und = 1,5 T in die
Gleichung ein und unterschlägt die Maßeinheiten
(die Physiker mögen mir diesen Frevel verzeihen), erhält
man die formal falsche aber praktisch nützliche Formel Û1
= 470 * A oder für die Effektivspannung Ueff =
333 * A . Soll z.B. ein Netztrafo gewickelt werden, dessen
Eisenkern einen quadratischen Querschnitt mit 4 cm Kantenlänge
hat, erhält man eine maximale effektive Umlaufspannung von U1
= 333 x 0,04 x 0,04 = 0,53 Veff. Bei 230 Volt
Netzspannung sind dann 433
Windungen zu wickeln.
1.2.3 Die Berechnung
der Drahtstärken eines Transformators
Als letzte Größe
wird der Drahtquerschnitt berechnet. Dazu wird den Spulen zunächst
ein Wicklungsquerschnitt zugeteilt. Üblicherweise erhält
die Primärspule etwa die Hälfte und die Sekundärspule(n)
die andere Hälfte des zur Verfügung stehenden
Wicklungsquerschnittes. Bei mehreren Sekundärspulen sollte der
Flächenanteil der einzelnen Spulen in etwa dem jeweiligen
Leistungsanteil entsprechen. Teilt man die zugeteilte Fläche
durch die Windungszahl, erhält man den theoretisch möglichen
Drahtquerschnitt der jeweiligen Wicklung. Wegen der zusätzlichen
Isolationen und sonstigen Lücken zwischen den Drähten wird
man aber nicht viel mehr als die Hälfte der zugeteilten Fläche
nutzen können. Durch präzise Wickeltechnik und rechteckige
Drahtquerschnitte lässt sich bei Serienprodukten der
sogenannte Füllfaktor noch deutlich erhöhen.
Da bei runden Kupferlackdrähten immer der Durchmesser angegeben wird, muss der Drahtquerschnitt noch in Durchmesser umgerechnet werden D = 2√A/π .