1.3. Der Streutransformator
Während die Streuung bei normalen Trafos ein unerwünschter Effekt ist, wird er Bei Streutrafos gezielt genutzt. Dabei ist mit Streuung nicht die Abstrahlung magnetischer Felder nach außen, sondern die künstliche Erhöhung der Streuinduktivität gemeint. Der Sinn der Streuinduktivität, die effektiv in Serie zum Verbraucher liegt, besteht darin, den Innenwiderstand des Trafos stark zu erhöhen, ohne den Spannungsabfall im Innenwiderstand als Wirkleistung verheizen zu müssen. Die Streuinduktivität kann dabei so hoch sein, dass der Trafo kurzschlussfest wird. Im Prinzip vereint der Streutrafo einen normalen Trafo und eine Vorschaltdrossel, ist aber wesentlich kleiner und leichter als beide Komponenten zusammen. Streutrafos sind für Verbraucher gedacht, die aufgrund ihrer Kennlinie oder sonstiger Eigenheiten eher mit einem konstanten Strom als mit einer konstanten Spannung versorgt werden müssen. Die bekanntesten Anwendung dürfte wohl die Versorgung von Gasentladungslampen sein (z.B. Hochspannungstrafos für Neonröhren). Das Funktionsprinzip des Streutrafos besteht darin, dass der magnetische Fluss, der durch die Primärspule fließt und von der Primärspannung erzwungen wird, über ein sogenanntes Streujoch der Sekundärspule ausweichen kann, wenn diese belastet wird.

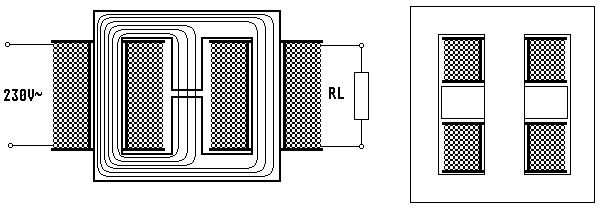
Bild 1.3 A Streutransformator in anschaulicher Bauweise

Bild 1.3 B Streutransformator in praktischer Bauform

Wichtiger Bestandteil des Streujoches ist der Luftspalt. Der Luftspalt stellt eine erhebliche Barriere für den magnetischen Fluss dar, sodass er den direkten Weg durch die Sekundärspule nimmt. Wird die Sekundärspule jedoch belastet, stellt auch sie eine größere Barriere für den Fluss dar; das durch den Sekundärstrom erzeugte Gegenfeld erhöht den effektiven magnetischen Widerstand des Kernes für den Fluss in der Sekundärspule. Ein Teil des magnetischen Flusses macht jetzt auch von der alternativen Möglichkeit Gebrauch, seinen Weg, an der Sekundärspule vorbei, durch das Streujoch und den Luftspalt zu nehmen. Die Länge des Luftspaltes und die Querschnittsfläche des Streujoches spielen für die Belastungskennlinie des Streutrafos die entscheidende Rolle. Die Querschnittsfläche des Streujoches bestimmt, einen wie großen Anteil des Gesamtflusses das Streujoch aufnehmen kann. Soll z.B. die Ausgangsspannung ohne Überlastung des Trafos bis auf zwei Drittel der Leerlaufspannung absinken dürfen, muss das Streujoch etwa ein Drittel des Gesamtflusses aufnehmen können und daher mindestens ein Drittel der Querschnittsfläche des eigentlichen Eisenkernes haben. Soll der Streutrafo kurzschlussfest sein, muss das Streujoch dementsprechend den gleichen Querschnitt haben wie der Hauptkern, damit es im Kurzschlussfall den gesamten Fluss weiterleiten kann. Der Luftspalt des Streujoches bestimmt direkt die Streuinduktivität, die für eine einwandfreie Funktion des angeschlossenen Verbrauchers stimmen muss. Für die praktische und die theoretische Bestimmung der Streuinduktivität wird die Sekundärspule kurzgeschlossen. Mit einem Induktivitätsmessgerät kann dann die primärseitige Streuinduktivität direkt an der Primärspule gemessen werden. Analog dazu wird die sekundärseitige Streuinduktivität an der Sekundärspule gemessen, während die Primärspule kurzgeschlossen ist. Das Verhältnis von primärer und sekundärer Streuinduktivität entspricht dem Quadrat des Übersetzungsverhältnisses.

Für die theoretische Berechnung geht man davon aus, dass das Eisen im Vergleich zur Luft keinen magnetischen Widerstand besitzt. Wenn die Sekundärspule kurzgeschlossen ist, muss der gesamte Fluss den Luftspalt überwinden. Da der Luftspalt nur kurz ist, kann des Magnetfeld darin als homogen angenommen werden, was die Berechnung erheblich vereinfacht. Um mir und dem Leser ein weiten Abstecher in die theoretischen Grundlagen magnetischer Felder zu ersparen, möchte ich auf die bekannte Formel für die Induktivität langer Luftspulen zurückgreifen. Zwischen dem Luftspalt und der langen Luftpule gibt es wesentliche Gemeinsamkeiten: Auch im Inneren der langen Luftspule ist das Magnetfeld homogen. So wie beim Luftspalt der magnetische Widerstand des Eisenkerns für den Rückweg des Flusses vernachlässigt werden kann, ist auch der Rückweg des Flusses außerhalb der langen Luftspule vernachlässigbar. Dies liegt daran, dass sich der Fluss axial durch die enge Spule zwängen muss, während ihm für den Rückweg außerhalb der Spule eine riesige Fläche zur Verfügung steht. Der magnetische Widerstand, der letztlich die Induktivität bestimmt, wird daher nur von Länge und Querschnittsfläche der Spule bzw. des Luftspaltes bestimmt. Es spielt also keine Rolle, ob man eine lange Luftspule oder eine Spule mit Eisenkern und Luftspalt berechnet. In beiden Fällen gilt die bekannte Formel: L = μ₀N²A/l mit L = Induktivität der Spule bzw. Streuinduktivität des Trafos, µ_o=4π*10^-7 (magnetische Feldkonstante), N = Windungszahl der Spule, A = Querschnittsfläche der Spule bzw. des Luftspaltes und l = Länge der Spule bzw. des Luftspaltes. Soll ein Streutrafo kurzschlussfest sein, muss die Streuinduktivität so dimensioniert werden, dass der im Kurzschlussbetrieb fließende Blindstrom den maximalen Betriebsstrom nicht überschreitet I = I_eff = U_eff/2π fL . Die minimale Streuinduktivität für Kurzschlussfestigkeit ist gleichzeitig auch die maximal sinnvolle für einen Streutrafo; wird die Streuinduktivität darüber hinaus erhöht, kann das Leistungspotential des Trafos nicht mehr genutzt werden. Die gleiche Wirkung ließe sich dann auch mit einem kleineren Trafo erzielen. In Bild 1.3 A ist die Anschauliche Version des Streutrafos dargestellt. In der Praxis findet man eher die Version aus Bild 1.3 B. Sie hat erstens den Vorteil, dass Standard-EI oder M-Kernbleche verwendet werden können und zweitens, dass wegen des kurzen Weges nur wenig zusätzliches Eisen für die beiden Streujoche erforderlich ist. Die Streujoche bestehen ebenfalls aus kleinen Blechpacketen, die so angeordnet sein müssen, dass die Einzelbleche parallel zur magnetischen Feldlinienrichtung liegen, in diesem Bild also horizontal. Die für die Berechnung der Streuinduktivität relevante Querschnittsfläche ist die Summe der Querschnittsflächen beider Streujoche. Die einfache Luftspaltlänge kann direkt in die Formel eingesetzt werden und sollte auf beiden Seiten gleich sein.

Wird ein Streutrafo vorwiegend mit konstanter Last betrieben (z.B. mit Neonröhre), ist es sinnvoll, den ständig fließenden induktiven Blindstrom mit einem Kondensator zu kompensieren. Vor allem bei großen Leistungen bzw. bei einer großen Anzahl von Trafos würde sonst der große Blindstromanteil zu einer erheblichen zusätzlichen Strombelastung im Wechselspannungsnetz führen.

1.4 Der Drehstromtransformator
Da die drei Drehstromphasen natürlich nicht in Phase sind, müssen sie beim Transformieren auf drei getrennten Spulenkörpern oder Transformatoren übertragen werden. Eine Besonderheit des Drehstromes liegt darin, dass sich bei symmetrischem Betrieb alle Ströme, auch die Magnetisierungsströme, im Mittelpunkt der Sternschaltung zu jedem Zeitpunkt kompensieren. Wenn dies für die Magnetisierungsströme gilt, gilt es natürlich auch für die dazu proportionalen magnetischen Flüsse in den drei Spulenkörpern. Wenn sich aber die drei Flüsse der drei Trafospulen immer aufheben, kann man sich eine einzelne Rückführung des Flusses an den drei Spulenkörpern sparen. Stattdessen werden die einander entsprechenden Spulenenden einfach mit einem gemeinsamen Eisenkern verbunden. Der Drehstromtrafo kommt daher mit wesentlich weniger Eisenmasse aus, als drei Einphasentrafos gleicher Gesamtleistung.

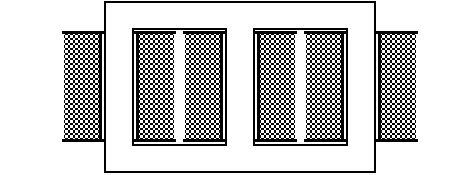
Bild 1.4 Anordnung der 3 Spulen auf dem gemeinsamen Kern eines Drehstromtransformators

In Bild 1.4 ist die Standardausführung eines Drehstromtransformators zu sehen. Der Kern sieht wie ein EI-Kern aus, besteht aber aus drei gleichgroßen Schenkeln. Auf den drei Schenkeln befinden sich die drei Spulenkörper für die drei Phasen. Bei der Beschaltung ist es sinnvoll, die Primärseite in Dreieck- und die Sekundärseite in Sternschaltung zu schalten. Das hat den Vorteil, dass der Sternpunkt auf der Sekundärseite voll belastbar ist, d.h. die drei Phasen der Sekundärspannung können beliebig asymmetrisch belastet werden. Mit einer speziellen Wicklungstechnik, bei der die Sekundärspulen auf alle Schenkel verteilt sind (Zickzack-Wicklung), erreicht man stets eine symmetrische Belastung der Eingangsspannung. Die Primärspulen können dann auch bei asymmetrischer Ausgangbelastung in Sternschaltung betrieben werden.

1.5 Der Spartransformator
Der Name verrät schon den Sinn eines Spartransformators oder auch Autotrafo genannt. Ist keine galvanische Trennung zwischen Eingangs- und Ausgangsspannung erforderlich, kann die Ausgangsspannung an einer Anzapfung der Primärspule entnommen werden. Da keine separate Sekundärspule nötig ist, steht der gesammte Wicklungsquerschnitt für die Primärspule zur Verfügung. Ein weiterer wesentlicher Vorteil ist, dass der volle Eingangs- und Ausgangsstrom nur durch einen Teil der Gesamtwicklung fließen muss, während er beim Trenntrafo durch Primär- und Sekundärwicklung fließt. Da der Spartrafo, genau wie der Trenntrafo, Leistung zwischen den beiden Teilwicklungen übertragen muss, werden auch den Teilwicklungen des Spartrafos je die Hälfte des Wicklungsquerschnittes zugeteilt. Beim Aufwärtsspartransformator wird eine Teilwicklung direkt mit der Eingangsspannung U_e verbunden. Die zweite Teilwicklung wird so geschaltet, dass sich ihre Spannung zur Eingangsspannung addiert.Diese zweite Wicklung muss den Ausgangsstrom I_a und die Differenz zwischen Eingangs- und Ausgangsspannung U_a vertragen. Die Trafoleistung muss dann mit P_t = (U_a-U_e) I_a = (U_a-U_e)P_a/U_a angesetzt werden. Soll also eine Ausgangsleistung P_a erzielt werden, ergibt sich die erforderliche Trafoleistung mit P_t = P_a(1 - U_e/U_a) . Wie man an der Formel erkennt, spart der Spartrafo besonders viel, wenn die Ausgangsspannung nicht viel größer ist als die Eingangsspannung. Ist das Übersetzungsverhältnis jedoch sehr hoch, lässt sich mit dem Spartrafo kaum sparen. Beim Abwärtsspartransformator werden einfach U_a und U_e physikalisch am Trafo und in der Formel vertauscht. Die erforderliche Trafoleistung ist dann entsprechend P_t = P_a(1 - U_a/U_e).
Als Grundlage für die Dimensionierung des Spartrafos dient die Trafoleistung P_t. Die Berechnung ist dann identisch mit dem Trenntrafo aus Kapitel 1.2 (siehe dort). Beispiel: Ein Verbraucher soll mit 250 Volt und einer Leistung von 500 Watt am 230-Volt-Netz betrieben werden. Ein Trenntrafo müsste eine Übertragungsleistung von 500 Watt vertragen. Der Spartrafo braucht dagegen nur 40 Watt übertragen.

1.6 Das Einschaltproblem von Netztransformatoren
Wie ich bereits in Kapitel 1.2.2 ausfühlich beschrieben habe, wird ein Netztrafo so dimensioniert, dass der Eisenkern gerade noch nicht in die Sättigung gerät. Im Normalbetrieb liegt am Trafo nach dem Nulldurchgang des Stromes, also auch des magnetischen Flusses, maximal eine viertel Periode (von 90°-180° oder von 270°-360°) der Wechselspannung an. Nach dem Nulldurchgang der Spannung baut sich das Magnetfeld dann wieder in jeweils umgekehrter Richtung auf. Es gibt jedoch zwei Effekte, die diesen periodischen Vorgang nachhaltig stören können. Der erste Effekt ergibt sich aus der Hysteresekennlinie des Eisens und er beginnt bereits beim Ausschalten des Trafos. Da der Eisenkern üblicherweise keinen Luftspalt besitzt, kann sich in ihm, trotz seiner weichmagnetischen Eigenschaften, auch nach dem Abschalten des Trafos noch ein beträchtlicher Restmagnetismus erhalten. Der zweite Effekt hängt mit dem Einschaltmoment zusammen. Im Idealfall müsste der Eisenkern im Einschaltmoment Feldfrei sein und die Spannung im Scheitelpunkt zugeschaltet werden. Nur dann kann man sicher sein, dass sich der in Kapitel 1.2.2 beschriebene Vorgang von Anfang an einstellt. Ist der Kern Feldfrei und wird die Spannung im Nulldurchgang zugeschaltet, steht dem Kern eine halbe Periode des Feldaufbaues bevor, was den doppelten magnetischen Fluss wie im Normalbetrieb bedeutet. Hatte der Restmagnetismus im Kern zu allem Überfluss auch noch die gleiche Polarität wie das sich jetzt aufbauende neue Feld, kommt der Kern noch vor Erreichen des ersten Scheitelpunktes der Spannung in die Sättigung. Die Primärinduktivität sinkt zuerst langsam, dann immer schneller auf vernachlässigbare Werte. Die Spannung liegt aber noch über eine viertel Periode in gleicher Richtung an der Primärspule an. Der Primärstrom wird dann nur noch durch den Kupferwiderstand der Primärspule und den Innenwiderstand der Eingangsspannung begrenzt. Bei großen Trafos ist es daher reine Glückssache, ob das Einschalten gelingt oder ob ein bzw. mehrere Gänge zum Sicherungskasten erforderlich werden. Bei kleineren Trafos (bis etwa 250 VA) ist das Problem weniger kritisch, da der höhere Drahtwiderstand der Primärwicklung nicht genügend Strom fließen lässt, um die in 230-Volt-Netzen gängigen 16-Ampere-Sicherungsautomaten auszulösen. Konstruktive Maßnahmen zur Vermeidung dieses Problemes wären zum einen ein Luftspalt zur Entmagnetisierung des Eisenkernes und zum anderen eine Verdoppelung des Kernquerschnittes. Der Luftspalt bewirkt eine Vergrößerung des Leerlaufblindstromes und der Leerlaufverluste. Die Verdoppelung des Kernquerschnittes bedeutet, dass der Trafo, bei gleicher Strombelastbarkeit, für die doppelte Spannung, also auch für die doppelte Leistung ausgelegt sein muss. In Bild 1.6 A sind Spannungs- und Stromverläufe für den Fall aufgetragen, dass der Trafo im ungünstigsten Moment, dem Nulldurchgang der Eingangsspannung, eingeschaltet wird. Die obere Kurve gibt die Eingangsspannung, z.B. die Netzspannung, ab dem Einschaltzeitpunkt an. Wäre die Spule und die Netzspannung verlustfrei bzw. ohne ohmschen Innenwiderstand, würde sich der in der mittleren Kurve dargestellt Strom einstellen. Die Entstehung dieser Kurve ist dadurch zu erklären, dass die Spule zunächst einer positiven Halbwelle voll ausgesetzt wird. Die folgende negative Halbwelle reicht dann gerade aus, den in der Spule aufgebauten Strom bzw. magnetischen Fluss wieder auf null zu kompensieren. Der magnetische Fluss erreicht also den doppelten Normalwert und ändert sein Vorzeichen nicht. Anschaulich kann man sich das als Überlagerung eines Gleichstromes mit dem halben Maximalwert vorstellen. Praktisch gibt es natürlich immer Verluste; der überlagerte und nur durch die Umstände des Einschaltens zustandegekommene Gleichstrom klingt exponentiell ab. Unter der Vorraussetzung, dass der Kern trotzdem nicht in die Sättigung gerät, erhält man dann in etwa den Stromverlauf der unteren Kurve.

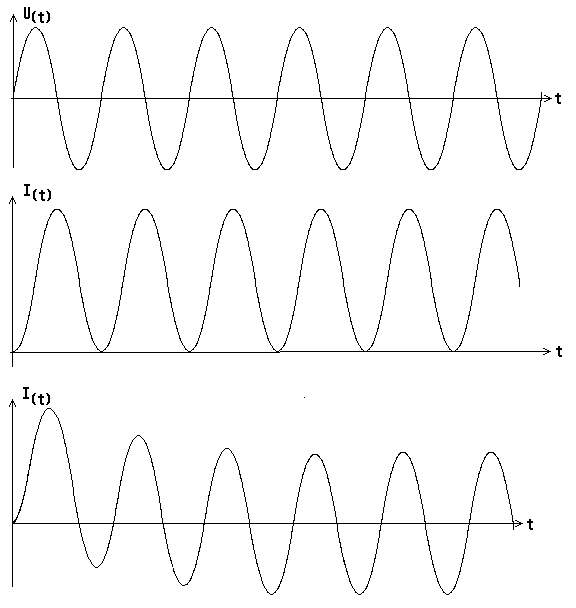
Bild 1.6 A Spannungs- und Stromverlauf einer Trafo-Primärspule, wenn der Trafo im Nulldurchgang eingeschaltet wird.

Oben: Verlauf der Spulenspannung ab dem Einschaltzeitpunkt

Mitte: Verlauf des Spulenstromes einer idealen Primärspule

Unten: Realer Verlauf des Spulenstromes ohne Kernsättigung

Wie schnell der überlagerte Gleichstrom abfällt, hängt vom Innenwiderstand der Spule und der Eingangsspannung ab. Je größer der gesamte Verlustwiderstand ist, desto schneller fällt der Strom ab. In der Praxis ist der Strom natürlich nicht sinusförmig sondern im Bereich der maximalen Stromwerte, insbesondere dort, wo noch der Gleichstrom überlagert ist, stark verzerrt. Durch die Abnahme der Induktivität im Bereich der magnetischen Sättigung steigt der Strom hier schneller an, was den Kern immer schneller in die Sättigung treibt. In der Praxis erkennt man diesen Effekt (nach dem Abklingen des Gleichstromanteiles) daran, dass die Stromkurve im Bereich der Scheitelpunkte spitz zuläuft. Die Lösung des Einschaltproblemes ist von der Leistung des Trafos abhängig. Bei kleinen Trafos (bis etwa 10 VA) spielt das Problem wegen des hohen Spulenwiderstandes keine Rolle. Bei Trafos bis etwa 250 VA muss man nur darauf achten, dass die Sicherung vor dem Trafo überdimensioniert und möglichst träge ist. Bei höheren Leistungen sollten zusätzliche Schutzschaltungen eingebaut werden. Die Schutzschaltung kann sehr einfach aufgebaut sein: Das Wirkungsprinzip besteht darin, dass der Innenwiderstand der Trafowicklung mit einem Serienwiderstand künstlich erhöht wird. Der Widerstand fängt die sättigungsbedingten Stromspitzen ab und lässt den überlagerten Gleichstrom nach wenigen Perioden abklingen. Tatsächlich ist die größte "Gefahr" bereits nach der ersten Periode gebannt. Der Serienwiderstand erlaubt einen Zusammenbruch der Spulenspannung bei Eintritt der Sättigung bis zum nächsten Nulldurchgang. Bei der nächsten Halbwelle ist der Kern dann bereits mit der umgekehrten Polarität magnetisiert und er kann mindestens eine viertel Periode entmagnetisiert werden. Das Magnetfeld wird so regelrecht auf die Netzspannung aufsynchronisiert. Um ständige Verluste im Widerstand zu vermeiden, wird er nach 100-200 ms mit einem Relais oder Triac kurzgeschlossen. Relais eignen sich jedoch besser, da sie eine besonders geringe Verlustspannung bei hohen Strömen haben. Die Bemessung des Widerstandes hängt von der Belastung des Trafos ab. Der Widerstand muss so hochohmig sein, dass die Netzsicherung nicht auslößt und so niederohmig, dass deutlich vor dem Einschalten des Relais fast die volle Wechselspannung an der Primärspule anliegt. Wird der Trafo im Einschaltmoment stark belastet, z.B. durch große Elkos oder Glühlampen, empfiehlt es sich, den Trafo erst zu belasten, wenn sich die Spannung mit dem Serienwiderstand aufgebaut hat und dieser kurzgeschlossen wurde. Der Serienwiderstand braucht dann nur noch den sehr geringen Leerlauf-Blindstrom ohne allzu großen Spannungsabfall durchzulassen; er kann so wesentlich hochohmiger ausfallen und daher die Stromspitzen besser abfangen.

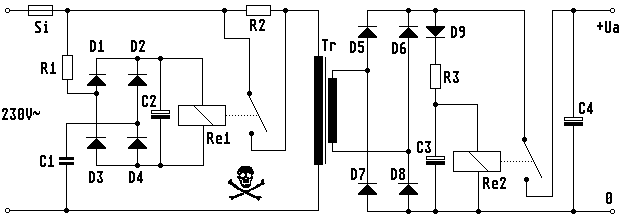
Bild 1.6 B Doppelte Einschaltverzögerung für große Netztransformatoren

Bild 1.6 B zeigt die einfache Ausführung einer doppelten Einschaltverzögerung für große Netztrafos. Die primärseitige Schaltung ist so ausgelegt, dass sie direkt von der Netzspannung versorgt wird und daher als eigenständiges Modul vorgeschaltet werden kann. Da Marktübliche Standardrelais bis 24 Volt Spulenspannung zu haben sind, muss der kapazitive Vorwiderstand C1 vorgeschaltet werden (ein ohmscher Vorwiderstand müsste min. 5 Watt verheizen). Der Blindstrom durch C1 wird mit dem aus D1-D4 bestehenden Brückengleichrichter gleichgerichtet und lädt den Siebelko C2. R1 schützt die Dioden D1-D4 vor den Einschaltstromspitzen in C1. Wenn die Spannung in C2 ausreichend hoch ist, zieht das Relais Re1 an und schließt den Schutzwiderstand R2 kurz. Kleine Relais bis etwa 15 Ampere Schaltstrom kommen mit etwa 30 mA Spulenstrom aus. Für die Dimensionierung kann man dann in etwa folgende Größenordnungen annehmen: R1 220 Ohm, C1 0,47 μF 250V~, D1-D4 1N4148 oder besser 1N4001, C2 100 μF 40V. Die Größe des Schutzwiderstandes R2 hängt sowohl von der Trafoleistung als auch von der Einschaltbelastung ab. Bei einem 1-kVA-Trafo mit doppelter Einschaltverzögerung kann er mit 47-100 Ohm 5W bemessen werden. Ohne sekundäre Einschaltverzögerung und großer Einschaltbelastung sind dagegen ca.10 Ohm 20W bei gleichzeitiger Vergrößerung von C2 auf 470-1000 µF angebracht. Nach dem Einschalten des Netztrafos wird auch C3 über D9 und R3 geladen. Die Bauteile müssen so bemessen sein, dass das Relais Re2 auf jeden Fall später anzieht als Re1. Re2 legt dann schließlich die sekundäre Last an den Trafo. Ein ohmscher Vorwiderstand R3 ist nur sinnvoll, wenn die Ausgangsspannung deutlich unter 100 Volt liegt; sonst empfiehlt sich die gleiche Schaltung, wie auf der Primärseite. Für einen noch sichereren Einschaltvorgang könnte man sogar eine vierstufige Sequenz ausführen:

1. Einschalten des Trafos mit Schutzwiderstand in der Primärspule
2. Kurzschließen des primären Schutzwiderstandes
3. Einschalten der Sekundärlast mit Vorwiderstand
4. Kurzschließen des sekundären Vorwiderstandes

1.7 50 Hz-Drosseln
50 Hz-Drosseln werden heute, zumindest in haustechnischen Leistungsbereichen, fast nur noch als Vorschaltgerät für Gasentladungslampen, meistens Leuchtstofflampen, verwendet. Im Prinzip kann eine Drossel aus einer Luftspule bestehen. Wie der Kondensator soll auch eine Drossel möglichst viel Energie auf kleinstem Raum speichern können. Die in der Spule gespeicherte Energie ist W_L = 0,5 L I². Der Strom ist durch die maximale Verlustleistung in der Spule begrenzt. In der Annahme, es handele sich um eine lange Spule, kann für die Berechnung der Induktivität wieder die bekannte Formel L = μ₀N²A/l mit L = Induktivität der Spule, µ₀=4π*10^-7Vs/Am (magnetische Feldkonstante), N = Windungszahl der Spule, A = Querschnittsfläche der Spule bzw. des Luftspaltes und l = Länge der Spule bzw. des Luftspaltes. Um die Speicherkapazität einer Spule zu erhöhen, kann man an mehreren Punkten ansetzen:

1. Windungszahl. Verdoppelt man z.B. die Windungszahl einer Spule, vervierfacht sich die Induktivität. Allerdings verdoppelt sich auch die Drahtlänge, während sich, bei gleichbleibenden Wicklungsquerschnitt, die Drahtquerschnittsfläche halbiert, was eine Vervierfachung des Spulenwiderstandes zur Folge hat. Bei gleicher Verlustleistung halbiert sich daher auch der maximale Spulenstrom. Bei vierfacher Induktivität und halbem Strom kommt man dann wieder auf die gleiche speicherbare Energie. Die "Speicherkapazität" einer Spule ist, bei gegebenem Wicklungsquerschnitt, deshalb unabhängig von der Windungszahl.
2. Spulenstrom. Um den Spulenstrom erhöhen zu können, müsste die Leitfähikeit des Drahtes erhöht werden. Eine unwesentliche aber sehr teure Verbesserung lässt sich durch Verwendung von Silberdraht, dem besten aller elektrischen Leiter, erzielen. Eine drastische Verbesserung der Leitfähigkeit, für den Hausgebrauch jedoch relativ unpraktisch, erreicht man noch mit supraleitenden Werkstoffen, die mit flüssigem Stickstoff oder Helium gekühlt werden müssen.
3. Permeabilitätszahl. Die magnetische Feldkonstante µ₀ , die eigentlich nur für Spulen im Vakuum, praktisch auch in der Luft gilt, muss noch mit der Permeabilitätszahl µ_r multipliziert werden. Wird der Raum um die Spule herum mit einem bezahlbaren ferromagnetischen Stoff z.B. Eisen ( µ_r ca. 10000 ) aufgefüllt, erhöht sich auch die Induktivität um diesen Faktor. Allerdings gerät das Eisen schon bei geringen Strömen in die Sättigung, lange bevor der zulässige Spulenstrom erreicht wird. Energie lässt sich im Eisen kaum speichern. Eine Alternative wäre noch die Verwendung von speziellen (Eisen)Pulverkernen, die in der Herstellung jedoch teurer sind, als normale Eisenkerne.
4. Abmessungen. Während eine Vergrößerung des Spulenquerschnitts auch die Gesamtausmaße der Spule erhöht, ist noch eine Verkürzung der Spulenlänge möglich. Wie ich bereits in Kapitel 1.3 bei den Streutransformatoren ausführlich erklärt habe, lässt sich die effektive Spulenlänge durch Verwendung eines hochpermeablen Eisenkernes mit Luftspalt auf die effektive Luftspaltlänge reduzieren. Die Drossel ist dann optimal dimensioniert, wenn beim maximal zulässigen Spulenstrom der Eisenkern gerade die Sättigungsfeldstärke des Eisens von etwa 1,5 Tesla erreicht wird. Dabei ist zu beachten, dass auch der max. zu erwartende reguläre Spitzenstrom noch nicht zur Kernsättigung führen darf. Nach den Gesetzen für magnetische Kreise, lässt sich dann der maximale Spulenstrom bei Eintritt der Sättigung ausrechnen: I_max = Bl/Nµ₀ mit B= Sättigungsfeldstärke (ca. 1,5 T),  l = Luftspaltlänge, N = Windungszahl und µ₀=4π*10^-7Vs/Am (magnetische Feldkonstante).

Die einfachste Bauform einer Drossel verwendet den EI-Kern. Dabei werden die E- und die I-Bleche jeweils zu einem Paket zusammengeklebt. Zwischen das E- und das I-Paket wird dann ein Pappscheibe als Abstandhalter gelegt. Pappe hat, wie die meisten Isolatoren, magnetische Eigenschaften, die sich kaum von Vakuum oder Luft unterscheiden. Da der magnetische Fluss die Pappscheibe am Mittel- und an den Außenschenkel, also zweimal durchdringen muss, ist die effektive Luftspaltlänge die doppelte Pappdicke. Die Querschnittsfläche entspricht der des Mittelschenkels.

weiter